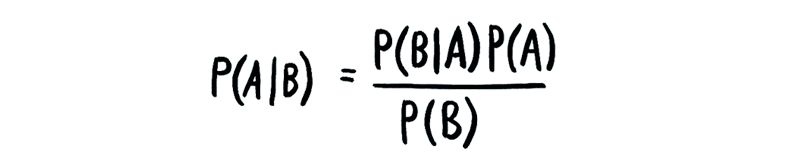- A+
本文谈到的贝叶斯定理是我在思考扑克局面时经常用到的工具,但我极少看到其他人谈论这个话题。因此,虽然我以前写过这方面的文章,但我觉得它值得更多关注。
贝叶斯定理(Bayes theorem)是概率论中的一个最基本概念。如果你初次接触贝叶斯定理,解释它的运作原理要比给出它的正式定义更简单。
假设有一个疾病测试,100个人中只有1个人患有这种疾病。你接受的测试有95%的准确度。你的测试结果是阳性,你患有这种疾病的可能性是多大?花点时间思考你的答案。
大多数人给出的答案是95%。这是不正确的——如你接下来将看到的,远非正确答案。
假设我们测试1万个人,在这1万人当中,100人患有这种病,而9900人没有这种病。当100个患病的人做这种测试时,我们得出95个阳性结果和5个阴性结果。当9900个没得这种病的人做这种测试时,我们得出495个阳性结果和9405个阴性结果。
因此,总共有590个阳性结果。在这些阳性结果当中,95人是患了这种病的,而495人是没得这种病的。如果你只知道你的测试结果是阳性,那么你患了这种疾病的机率是95/590 = 0.161,或者说16%。
如果这个概念对你来说很新鲜,那么再次回顾上面的例子。你对于某种疾病的测试是阳性,测试准确度是95%,但你真正患上这种病的概率只有16%。
这种差异是因为这种疾病相对稀少。只有1/100的人真正患上这种病。但5/100的测试者将得到错误的结果。因此,这种测试很容易得出错误的结果。
如果我们改变这个例子,将这种疾病的流行度降至1/1000,那么一个精确度95%的阳性测试结果只给你2%的机率真正患了这种病。
这是一个有点反直觉但极有用的概念。
接下来我将向你分享一个扑克场景,然后做出类似上面的推理,让你体会贝叶斯定理在牌桌上的应用。
假设在河牌圈,你的对手在800美元的底池下注500美元。你有一手抓诈牌。如果他有自己试图代表的牌,那么你输。但他可能在诈唬。你应该跟注吗?
底池赔率告诉你,你需要在28%的时候获胜,才能证明跟注是合理的。那么对手需要在28%的时候诈唬。如果他的诈唬低于这个频率,你弃牌;高于这个频率,你跟注。
这里存在两个相关的信息片段。首先,当该牌手拿着一手破灭的听牌时,他诈唬的可能性有多大。这显然与我们的决定相关,但许多人在做决定时卡在了这里。“他是否一个爱诈唬的人?若是,跟注,若否,弃牌。”
但你也需要另一个信息片段——他可以代表多少种底牌组合,这些组合占据他整个范围的百分比是多少。
假设说公共牌面存在同花可能,你认为对手要么拿着同花,要么在诈唬。你觉得他会用总共100种可能的底牌组合打到河牌圈。其中20种组合是同花,另外30种组合是他不会下注的顶对和两对,但他也不会用它们去诈唬。其余50种组合是适合去诈唬的破灭的听牌。
他在800美元的底池下注500美元。你应该跟注吗?
假设他会用全部20种同花组合下注。你需要在28%的时候获胜,才能证明跟注是合理的,那么为了使你的跟注正确,对手必须至少用8种组合去诈唬(因为8/28 = 28.6%)。
你认为他有50种候选的诈唬牌。他需要用其中的至少8种组合真正诈唬。相关问题是:“该牌手看到候选的诈唬牌时真正去实施诈唬的频率是多少?”如果你的答案是“至少16%的时候,”那么你的对手将用50种诈唬组合中的至少8种去诈唬,因为你可以预计在至少8/28的时候获胜,你可以跟注。
我想在这里提出两个相关数字。
首先是28%(对手的诈唬概率)。这个数字是视情况而定的。也就是说,对手的下注是否在28%的时候是诈唬取决了他的起手牌范围。如果他一开始就有一个很强的范围,那么他不太可能在28%的时候诈唬,因为他有那么多好牌,他必须疯狂诈唬才能让诈唬频率达到28%。
第二个数字16%完全取决于牌手。这个对手是那种在机会来临时愿意在至少16%的时候做大诈唬的人吗?一个在16%的时候诈唬的牌手,其诈唬频率往往与他的起手牌范围是好是坏无关。
假设我们打2/5美元的牌局,而且我们认为对手比较紧弱(nitty)。你不会指望他在得到机会的时候16%的时候做诈唬全压。
相反,你认为这个数字更可能是5%。大多数时候他会冷静地接受失败,但偶尔他会鼓起勇气放飞自我(诈唬)。
这是我们很少希望去跟注的牌手。
但假设使他置身于一种极端情况下,比如你们在竞争一个底池,他全压。这次他不是代表同花,而是代表葫芦这样极少见的牌。因为底牌排除效应和他没有打过特定牌局的事实,只有5种他可能拿到的组合能够使价值下注成立。假设他有45种“因为太好而不能诈唬,但又不够好到下注”的底牌组合。然后,他有60种候选的诈唬牌组合。
他在5%的时候诈唬,因此在60种候选的诈唬牌组合中,他只用其中3种组合去诈唬。
因此,当他下注时,他5/8的时候拿着强牌,3/8的时候在诈唬。他在这种场合的总诈唬频率是37.5%——所以,你应该跟注他的500美元下注。这是正确的,即使他是一个很少诈唬的紧弱牌手!因为他能代表的好牌非常少,他的价值下注牌只比更稀少的诈唬牌多一点。
需要澄清的是,牌手只有五种价值下注组合的情况很少见。因此,绝对不要说,在紧弱玩家下大注时你应该跟注他们。恰恰相反,通常你应该弃牌。但为了做出那种决定,知道对手紧弱和极少诈唬还不够。知道他代表的牌有多常见/少见也很重要。如果极其少见,你甚至要考虑跟注一个紧弱玩家。
作者简介
Ed Miller是著名的扑克书作者,专长是小注额现金桌,著述的扑克书籍销量超过25万册。他曾在麻省理工学院主修电子工程和物理,后入微软,不过最终辞职做了职业牌手和扑克写手。他并不是一直都是赢家,也曾有由错误中学习的经历。最后成为了一代高手。他的著作大家肯定阅读过不少,绝对是每本都是经典,包括:《Small Stakes No-Limit Hold’em》、《Professional No-Limit Hold’em: Volume I》、《Small Stakes Hold’em:Winning Big With Expert Play》、《No Limit Hold’em:Theory and Practice》、《Playing the Player》等。Ed Miller目前是扑克培训网站CardPlayer的专栏写手。